Enhanced Predictive Modeling for Neuromuscular Disease Classification: A Comparative Assessment Using Gaussian Copula Denoising on Electromy-ographic Data

Enhanced Predictive Modeling for Neuromuscular Disease Classification: A Comparative Assessment Using Gaussian Copula Denoising on Electromyographic Data

Eduardo Cepeda ^1*, Nadia N. Sánchez-Pozo ^1,2, Liliana M. Chamorro-Hernández ¹

¹Universidad Politécnica Estatal del Carchi, Tulcán 040102, Ecuador;

{eduardo.cepeda, nadia.sanchez, lilianam.chamorro}@upec.edu.ec

² Mondragon University, Mondragón 20500, España;

n.sanchez@mondragon.edu

* Correspondence: educepedam@gmail.com

ABSTRACT

This study presents a methodology for automatically detecting neuromuscular diseases through preprocessing and classifying electromyography (EMG) signals. The presented approach integrates Gaussian Copula-based denoising techniques with feature extraction and Random Forest classification. To assess the performance, the study performs a comprehensive evaluation of various denoising techniques, including Empirical Mode Decomposition (EMD), Variational Mode Decomposition (VMD), Wavelet Thresholding Denoising (WTD), and Gaussian Copula Denoising (GCD). The study also compares the effectiveness of several classification algorithms, such as Random Forest (RF), Convolutional Neural Networks (CNN), Multilayer Perceptron (MLP), and Decision Tree (DT). The methodology demonstrated exceptional performance, achieving an overall accuracy greater than 99% in distinguishing between healthy, myopathic, and neuropathic EMG signals. The proposed method's effectiveness is attributed to its noise reduction capabilities, feature selection focusing on mean amplitude and amplitude range, and the Random Forest algorithm's adeptness in classifying EMG data. The study's findings underscore the proposed method's accuracy and effectiveness and highlight its potential to revolutionize clinical diagnostics of neuromuscular disorders, offering a powerful tool for more precise and timely interventions.

Keywords: Electromyography; Denoising; Classification; Neuromuscular Diseases; Gaussian Copula; Random Forest; EMG; CNN.

INTRODUCTION

The backbone of science, technological advancement, and information dissemination are signals. These signals manifest as patterns with varying amplitudes and frequencies, spanning fields from telecommunications to biomedical engineering. Analyzing and interpreting these signals is crucial yet challenging, requiring methods to extract key features from noisy datasets. This process involves understanding signal relationships, identifying meaningful patterns amid interference, and tailoring techniques for specific applications¹. One significant challenge in electromyography (EMG) applications is the early detection of neuromuscular diseases (NMD). Individuals with NMD face a broader spectrum of chronic illnesses and health symptoms compared to the general populace². Delays in diagnosing and identifying these diseases can result in severe consequences, including reduced treatment effectiveness and a more substantial negative impact on the patient's quality of life³. Muscle recruitment timing is crucial for developing electromyography-powered assistive devices, clinical analyses, and muscle-machine interface applications.

Traditionally, muscle activation identification relies on visual inspections by trained experts, which are time-consuming, non-reproducible and impractical for large datasets⁴. These traditional methods are also susceptible to human error, compromising the accuracy of results. Acquiring detailed information about human health is the primary goal of collecting, preprocessing, and analyzing physiological signals. These signals, covering many biological parameters, offer a comprehensive view of human body function^5,6. Changes in these signals and the normal and abnormal physiological processes they represent have broad applications in medicine. These include clinical diagnosis, ongoing patient monitoring, assessing treatment effectiveness, and developing new biomedical signal preprocessing techniques⁷. Despite advancements in semi-automated techniques, challenges persist in preprocessing physiological signals, particularly electromyography (EMG)⁸.

These methods often require manual input to optimize detection algorithm parameters and necessitate adjustments for each muscle group, individual, and movement, rendering them inefficient for large-scale data preprocessing⁹. Moreover, the nature of EMG signals introduces considerable variations in signal-to-noise ratios (SNR) between different muscle groups, complicating the detection of neuromuscular diseases^10,11. EMG denoising methods have fundamentally addressed these challenges, especially when combined with implementing artificial intelligence techniques¹². This synergy has become indispensable for accurately interpreting, classifying, and detecting EMG signals. Currently, research has focused on addressing this problem comprehensively, ranging from gesture classification and early detection of muscle fatigue to applications of machine learning techniques, all enhanced by improved signal quality achieved through reducing noise techniques^13,14. Recent advancements in signal denoising have focused on three principal techniques: Empirical Mode Decomposition (EMD)^13,15,16, Variational Mode Decomposition (VMD)^17–19, and Wavelet Thresholding Denoising (WTD)^20–22.

These approaches have remarkably addressed complex signal preprocessing challenges, particularly for intricate biomedical signals like EMGs. EMD, designed for non-linear and non-stationary signals, decomposes waveforms into Intrinsic Mode Functions (IMFs), proving particularly advantageous for noise reduction in complex signals^15,23.

VMD, decomposes signals into a predetermined number of oscillation modes, overcoming limitations of EMD such as noise sensitivity and challenges in discriminating between closely spaced frequency components¹⁷. WTD employs wavelet transformation to attenuate noise by applying threshold parameters to wavelet coefficients, utilizing both soft and hard thresholding approaches²⁴. Among this domain's most prevalent classification modelsupport Vector Machine (SVM)¹¹, Convolutional Neural Networks (CNN)²⁵ and Random Forests²⁶. These methodologies are frequently employed for multiclass classification tasks, offering sophisticated approaches to complex data analysis. Despite these advancements, the field of muscle activation remains relatively unexplored, presenting challenges in EMG signal preprocessing, feature selection, and identifying optimal models for classifying neuromuscular diseases²⁷. Artificial intelligence, including machine learning and deep learning techniques²⁸, has shown promise in classifying electromyography signals^29,30. A critical aspect of improving EMG signal analysis is addressing the noise introduced during signal acquisition³¹. Various exogenous and endogenous factors, including myoelectric contractions and electromagnetic interference from power grids, combined with the inherent stochasticity of physiological signals, can significantly compromise data quality^32,33. To mitigate these issues, reducing noise methodologies have been developed.

Table 3 presents a comprehensive overview of the most effective signal preprocessing and classification methodologies employed to achieve the objective mentioned above. These methods include: k-Nearest Neighbors (K-NN) implementing tunable-Q factor wavelet transform (TQWT) as a preprocessing step³⁴; Support Vector Machine (SVM) using Sample Entropy (SE) and Mean Absolute Deviation (MAD) as feature extraction techniques¹¹; Binarized Neural Network (BNN) employing Fast Fourier Transform (FFT) preprocessing³⁵; Machine Learning (ML) pipeline leveraging Motor Unit Potentials (MUPs) for preprocessing³⁶; Deep Learning (DL) incorporating Butterworth filter (BF) preprocessing³⁷; Random Forest (RF) with Fast Fourier Transform (FFT) preprocessing³⁸; and Machine Learning (ML) utilizing signal-to-noise ratio (SNR) analysis for preprocessing³⁹; This diverse array of approaches demonstrates the ongoing evolution and refinement of signal processing and classification techniques in the field.

Kiran PU et al.³⁴ conducted a study focusing on classifying electromyography (EMG) signals from individuals with amyotrophic lateral sclerosis (ALS) and healthy subjects. The research utilized tunable-Q factor wavelet transform (TQWT) features. The methodology involved decomposing EMG signals into sub-bands using TQWT and extracting statistical features, including mean absolute deviation (MAD), interquartile range (IQR), kurtosis, mode, and entropy. These features were subsequently evaluated using k-Nearest Neighbors (K-NN) classifiers. The proposed approach demonstrated enhanced classification performance compared to existing methods, achieving a classification accuracy of 0.95.

Abdul Wadud et al.¹¹ developed a feature extraction and classification model for distinguishing between healthy and myopathic EMG signals. The research employed a comprehensive approach to signal preprocessing, encompassing normalization via bandpass filtering and subsequent signal segmentation into frames. The feature extraction phase employed two primary techniques: Sample Entropy (SE), which quantifies signal complexity and regularity, and Mean Absolute Deviation (MAD), which assesses data variability relative to its meaning. Mean Squared Error (MSE) was calculated to optimize classification performance to determine the most compelling feature. The final classification step utilized SVM classifiers to differentiate between standard and myopathic cases. The model's efficacy was evaluated, and an accuracy of 0.99 was obtained.

Soongyu Kang et al.³⁵ developed a hand gesture recognition system based on surface electromyography (sEMG) technology. Their signal preprocessing methodology involved transforming raw sEMG data into spectrograms, effectively capturing time-frequency domain information. The spectrogram generation process employed a 128-point Fast Fourier Transform (FFT) with a Hamming window and 50% overlap. For the classification task, they implemented a binarized neural network (BNN) on a field-programmable gate array (FPGA), leveraging the efficiency of this lightweight convolutional neural network (CNN) variant. This proposed system achieved a classification accuracy of 0.95.

M.R. Tannemaat et al.³⁶ conducted a study utilizing a time series classification algorithm to differentiate between normal, neuropathic, and myopathic electromyography (EMG) tracings. The signal preprocessing phase involved a visual examination of the raw trace to identify the most suitable continuous fragment containing motor unit potentials (MUPs), ensuring the absence of needle movement, 50 Hz artifacts, or other disturbances. Subsequently, 5-second EMG fragments were extracted from each muscle for analysis. The study employed a machine learning (ML) pipeline as the primary classification method. In distinguishing EMGs of healthy individuals from those with ALS, an accuracy of 0.834 at the muscular level and 0.856 at the patient level was achieved.

The study conducted by Xiaoyuan Luo et al.³⁷ implemented a gesture recognition performance utilizing surface electromyography (sEMG) signals. They developed a Deep Learning (DL) approach based on ResNet50. For sEMG signal preprocessing, the researchers implemented a full-wave rectifier followed by a Butterworth filter (BF) to eliminate noise, a critical step in optimizing signal quality before analysis. The classification methodology incorporates multi-scale modules and self-attention mechanisms within the ResNet50 architecture, thereby improving the extraction of channel feature information from sparse sEMG signals. The study yielded promising results. When evaluated on the NinaPro DB1 and NinaPro DB5 datasets, the model achieved recognition accuracies of 0.8794 and 0.8704, respectively. Furthermore, in predicting the grasping mode of an electromyographic manipulator, it attained an accuracy of 0.8837.

The research conducted by Pranav Madhav Kuber et al.³⁸ investigated fatigue detection during exoskeleton-assisted trunk flexion tasks utilizing machine learning techniques. The methodology involved preprocessing data by extracting 135 features from muscle activity recordings, trunk motion measurements, and whole-body stability assessments across various segments of each trunk-flexion cycle. Feature extraction techniques included Fast Fourier Transform (FFT) for frequency domain analysis and Root Mean Square (RMS) for EMG signal processing. The study employed the Random Forest (RF) classification algorithm. Results indicated that RF demonstrated significant efficacy in classifying fatigue using data from a single EMG sensor positioned on the lower back muscle. This approach yielded an accuracy of 0.92, and a recall of 0.91.

The study conducted by Iqram Hussain et al.³⁹ implemented a preprocessing methodology for electromyographic (EMG) signals using signal-to-noise ratio (SNR) analysis. This process encompassed noise filtration through SNR, allowing for identifying and eliminating EMG epochs exhibiting insufficient signal quality, with particular emphasis on those affected by low-frequency motion artifacts. Gait signals from 48 stroke patients and 75 healthy controls were analyzed. The researchers employed Machine Learning (ML) methodologies to develop an interpretable framework. This framework was designed to accurately distinguish between the characteristic myoelectric patterns observed in stroke patients and those of healthy individuals.

The best classification model demonstrated a performance metric of 0.94 during cross-validation with the training dataset. Upon evaluation using the EMG test dataset, the model achieved an accuracy of 0.92 and a precision of 0.85. Despite advancements in EMG signal preprocessing, clinical implementation remains challenging due to issues such as biases and overtraining⁴⁰. This study tackles these challenges by optimizing signal preprocessing through Gaussian Copula Denoising. It aims to identify the ideal combination of this innovative preprocessing technique with suitable machine learning algorithms and EMG signal feature selection. The objective is to assess the effectiveness and precision of this approach in diagnosing neuromuscular diseases.

Gaussian copulas have emerged as a powerful statistical tool, gaining widespread adoption across diverse fields. Their applications include feature reduction in multi-parameter fusion methods for blood pressure estimation⁴¹, multidimensional synthesis in electronic systems⁴², complex signal analysis, where the signals exhibit intricate dependency structures⁴³. These applications demonstrate the versatility and effectiveness of Gaussian copulas in handling intricate data structures and dependencies. This study employs Gaussian copulas as an advanced method to capture and model the complex dependencies inherent in EMG signal data. This statistical approach enables a more refined and comprehensive understanding of the multifaceted relationships present in EMG signals, potentially yielding more accurate, reliable, and insightful analyses. The noise reduction process for EMG signals using Gaussian copulas involves a systematic approach that capitalizes on the inherent dependency structure within the data. This process encompasses several key steps: signal segmentation, rank transformation, Gaussian copula fitting, correlation matrix estimation, copula-based filtering, and finally, reconstruction of the noise-reduced signal.

The decision to utilize Gaussian copulas for EMG signal preprocessing is grounded in their exceptional capacity to model multivariate distributions effectively, even in challenging scenarios where the underlying marginal distributions significantly deviate from Gaussian norms⁴⁴. This attribute is precious in biomedical signal processing, where data often exhibit highly intricate non-linear relationships and complex interdependencies. The adaptability of Gaussian copulas to non-Gaussian distributions renders them exceptionally well-suited for addressing the multifaceted complexities frequently encountered in EMG signals, which a wide array of physiological and environmental factors can influence. The Random Forest classification algorithm will be employed as a benchmark for performance assessment to evaluate the efficacy of the Gaussian copula denoising method. This machine learning technique will be utilized to classify the preprocessed EMG signals, allowing for a comprehensive comparison of classification accuracy between the Gaussian copula approach and other noise reduction methods. By leveraging the Random Forest algorithm's inherent ability to handle high-dimensional data and capture complex non-linear relationships, we aim to provide a thorough and unbiased assessment of the Gaussian copula denoising method's impact on signal quality and subsequent classification performance. This comparative analysis will not only elucidate the relative merits of our proposed approach but also contribute valuable insights to the broader field of biomedical signal processing.

The paper is structured as follows: Section 2 details the implemented methodology, including data acquisition, signal preprocessing, segmentation and feature extraction, classification models, and performance metrics. Section 3 presents the complete experimental results. Section 4 analyses and compares the performance of different methods used to classify healthy, neuropathy, and myopathy signals. Finally, the conclusions are provided in Section 5.

MATERIAL AND METHODS

The schematic representation of the generic electromyographic (EMG) detection system presented in Figure 1, designed to achieve the main objective, begins with acquiring the EMG signal. In our research, this signal is obtained from the Physionet database⁴⁵. Subsequently, the signal undergoes a preprocessing phase, followed by a segmentation and characterization stage. Next, classification is implemented using advanced machine-learning techniques. Finally, evaluation metrics are applied to determine the accuracy and effectiveness of the proposed system. This methodological approach integrates key stages for robust analysis of EMG signals, facilitating information extraction and precise pattern identification.

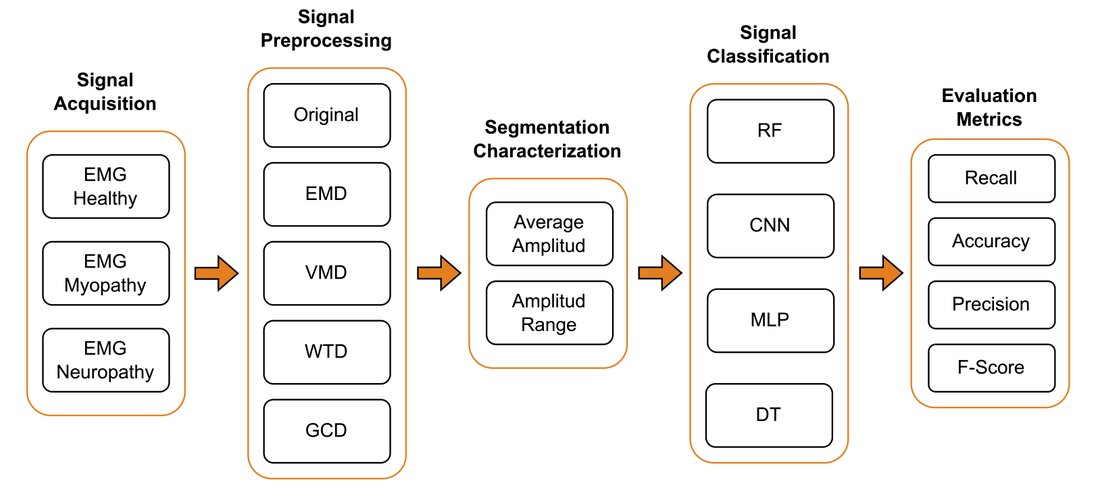
Figure 1. Electromyographic detection systems encompass signal acquisition, preprocessing, segmentation, characterization, classification, and evaluation metrics aimed to achieve the primary objective.

To determine the most effective method for detecting neuromuscular diseases, data denoising based on Gaussian Copula Denoising (GCD) was employed and tested. This method is essential to remove unnecessary signal noise by rescuing the relevant to identify the underlying patterns in EMG signals, which are crucial for accurate disease detection. The study commenced with the acquisition of EMG data using the Physionet Base Data website⁴⁵. Following data acquisition, thorough preprocessing was conducted, including noise filtering and data normalization, to maintain consistency across different samples. Four different methods for noise filtering were tested including innovative Empirical Mode Decomposition (EMD), Variational Mode Decomposition (VMD), Wavelet Thresholding Denoising (WTD), and Gaussian Copula Diagnosing (GCD).

Characteristics of the data were then extracted, including mean amplitude and amplitude range. After feature extraction, classification was performed using Random Forest (RF), Convolutional Neural Networks (CNN), Multilayer Perceptron (MLP), and Decision Tree (DT) methodologies. The classification models were evaluated using standard metrics such as Recall, Accuracy, Precision, and F-Score. This evaluation was pivotal in assessing model performance and involved a comprehensive analysis of various performance indicators.

Finally, the models were compared using the evaluation as mentioned earlier metrics. This comparison was instrumental in identifying the most effective method for detecting neuromuscular diseases, offering valuable insights into each approach's strengths and weaknesses. The detailed analysis of these metrics ensured the chosen model was accurate but also reliable and robust across various testing conditions.

Data acquisition

The study utilizes EMG signals to investigate neuromuscular diseases, encompassing both neuropathy and myopathy. These signals, available on the Physionet Base Data website⁴⁵, were carefully collected using an Oxford Instruments Medical Medelec Synergy N2 EMG monitoring system¹⁵. The dataset comprises individuals both with and without neuromuscular conditions. Specifically, data were obtained from three patients: a 44-year-old man with no neuromuscular disease history, a 62-year-old man with chronic low back pain and neuropathy due to right L5 radiculopathy, and a 57-year-old man with myopathy resulting from polymyositis. The EMG signals were initially captured at a sampling frequency of 50 KHz (50,000 Hertz), allowing for a detailed signal representation with 50,000 samples per second. Subsequently, the data were down-sampled to 4 KHz (4,000 Hertz) to facilitate a more manageable analysis. This down-sampling is particularly useful as higher frequencies often do not contribute significant additional information⁴⁶.

The database selection for this study was based on several critical factors that ensure robustness and relevance. Firstly, the chosen database contains EMG signals from healthy subjects, myopathy patients, and neuropathy, which aligns perfectly with our objective of classifying neuromuscular diseases. This clinical relevance is paramount for the applicability of our findings. Additionally, the database is widely recognized and utilized within the scientific community, guaranteeing the quality and reliability of the data, which is crucial for the validity of our results. Furthermore, using a standardized database facilitates direct comparison of our results with other studies in the field, enhancing the validation and reproducibility of our research¹⁹. While other EMG signal databases exist, the one selected for this study offers the optimal balance between clinical relevance, data quality, and applicability to our specific research objectives. This careful selection process underscores our commitment to conducting rigorous and impactful research in neuromuscular disease classification⁴⁷.

Signal preprocessing

During the data recording process, a 20 Hz high-pass filter and a 5 KHz low-pass filter were applied. The high-pass filter removed frequencies below 20 Hz, while the low-pass filter excluded frequencies above 5 KHz. These filtering steps were crucial for eliminating noise and irrelevant signals outside the target frequency range, ensuring the collected data was clean and precise. This meticulous approach enhances the accuracy of studies related to neuromuscular diseases, thereby facilitating better understanding and treatment. Subsequently, a normalization procedure was executed to nullify negative data values, followed by a thorough comparative analysis of four distinct noise reduction methodologies for EMG signal refinement, including innovative Empirical Mode Decomposition (EMD), Variational Mode Decomposition (VMD), Wavelet Thresholding Denoising (WTD), and Gaussian Copula

Diagnosing (GCD)

The primary objective of this evaluation was to identify the most efficacious technique for noise attenuation while preserving critical signal characteristics. This approach is paramount for maintaining the integrity of clinically pertinent information, thereby optimizing feature extraction by mitigating noise interference while keeping the temporal structure of the signal. Consequently, this enables a more nuanced extraction of salient features for the subsequent classification of neuromuscular pathologies based on EMG signals. These pivotal steps adequately prepare the signal for ensuing segmentation and feature extraction processes. This holistic and methodical approach is essential for ensuring the reliability and reproducibility of research outcomes, thereby establishing a robust foundation for future investigative endeavors and potential clinical applications in neuromuscular diagnostics¹⁸.

Empirical Mode Decomposition

This groundbreaking study harnesses the power of an innovative Empirical Mode Decomposition (EMD) denoising function. The EMD process, with its remarkable adaptability, deftly separates the signal Into a finite array of oscillatory components, each serving as a distinct, high-resolution snapshot of the original signal's multifaceted structure:

wherein signifies the Intrinsic Mode Functions (IMFs) and embodies the residual component. Following this decomposition, the function artfully reconstructs the signal by amalgamating all IMFs, with the notable exclusion of the first. This judicious reconstruction is predicated on the principle that the inaugural IMF typically encapsulates the highest frequency components, which frequently correspond to extraneous noise or undesirable artifacts in EMG signals. By excluding this component, the function effectively attenuates high-frequency noise while preserving the quintessential characteristics of the EMG signal. To enhance computational efficiency, the EMD denoising process uses parallel computing techniques. This approach speeds up processing time for large EMG datasets. The EMG signals are divided into manageable batches, each processed independently on separate cores. The total processing time T can be estimated as:

Where N is the total data points, B is the batch size, C is the number of cores used, t is the time to process one batch, and O is the overhead time. This method optimizes resource use and allows efficient processing of large datasets. It processes EMG data segments simultaneously, reducing overall processing time while maintaining denoising quality for each batch^16–19.

Variational Mode Decomposition

We employ Variational Mode Decomposition (VMD) as a signal-denoising technique to separate signals into distinct oscillatory modes. This method is implemented through a custom function designed for electromyographic (EMG) signal preprocessing, addressing the challenges in EMG data analysis. The VMD function decomposes the input EMG signal into Intrinsic Mode Functions (IMFs), each representing a unique frequency component. Mathematically, VMD is formulated as an optimization problem:

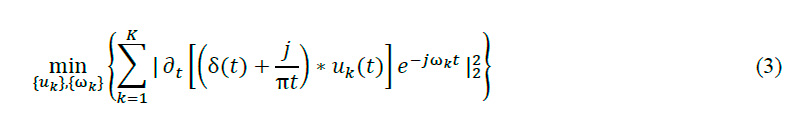
In this formulation, represents modes, center frequencies, the function involves the input signal, and k is the number of modes. This framework enables accurate EMG analysis. The function reconstructs the signal by removing high-frequency noise and excluding lower-frequency with less relevant information. This approach, balances noise reduction and preservation of key signal features. It is particularly effective for EMG signals, where important information is often within a specific frequency range. The result is a refined signal that maintains essential features of the original EMG recording, enabling more accurate analysis and classification of neuromuscular diseases. This method significantly improves EMG signal preprocessing, potentially enhancing diagnostic accuracy in clinical neurology and advancing neuromuscular disease classification^17,18.

Wavelet Thresholding Denoising

The methodology for preprocessing EMG signals using Wavelet Thresholding Denoising (WTD) enhances signal fidelity for more precise analysis. The process involves several key stages⁴⁸, starting with the spectral decomposition. Applies Discrete Fourier Transform (DFT) to decompose the EMG signal into frequency components:

Where is the input signal, is the transformed signal, N is the total samples, k is the frequency index, and n is the temporal index. Frequencies are calculated as:

With as frequency in Hz and fs as sampling frequency (1000 Hz). The magnitude spectrum is computed by:

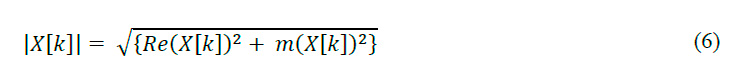
Regarding wavelet denoising, this process employs VisuShrink thresholding. A wavelet decomposition was performed using Discrete Wavelet Transform (DWT). This transforms the signal into wavelet coefficients at different scales and positions. Then, the VisuShrink threshold, which is an adaptive threshold based on the noise level of the signal, was calculated. This threshold was then applied to the wavelet coefficients using a soft threshold, which helps remove noise while preserving important signal features. Finally, the signal was reconstructed using Inverse Discrete Wavelet Transform (IDWT). Then, signal reconstruction, after noise removal, inverse wavelet transform (IWT) was used to recover the signal. The coefficients were first augmented by zero insertion. Then, convolution was performed with reconstruction filters, and finally, the convolution results were added to obtain the reconstructed signal^49,50.

This comprehensive methodology is applied to healthy, myopathic, and neuropathic EMG signals. It incorporates Spectral Decomposition for frequency analysis, Wavelet-based Noise Reduction for signal cleaning, Adaptive Thresholding for noise level adjustment, and Signal Reconstruction for obtaining the final processed signal. The entire process significantly reduces noise in EMG signals while preserving important signal characteristics. This enhancement of data integrity is crucial for a more reliable classification of neuromuscular pathologies. Improving signal quality ensures accurate diagnosis and monitoring of neuromuscular conditions in the fields of electromyography and clinical neurology.

Gaussian Copula Diagnosing

This study aims to implement a Gaussian copula-based denoising method to enhance the quality of EMG signals. This approach utilizes sliding windows and rank transformations to fit a Gaussian copula to the data. The denoising method employed in this study, grounded in Gaussian copulas, was designed to elevate the quality of EMG signals to unprecedented levels. The size of these windows is configurable, with a default value of 1000 samples used in this case, allowing for granular and adaptable signal analysis.

Specialized data structures were initialized, including vectors to store the processed (denoised) signal and corresponding indices for valid samples. The window preprocessing algorithm iterates over each segment of the EMG signal, applying a comprehensive set of transformations to each window. A crucial step in this process is the application of the probability integral transform, where represents the empirical distribution function, denotes the window values, and n is the number of samples. This transformation converts the original data to a uniform scale between 0 and 1, which is indispensable for the subsequent application of copula techniques.⁵¹

For copula fitting, we employed the density function of the Gaussian copula, where \Phi represents the correlation parameter, and x, y are derived from , , with being the inverse of the standard normal distribution function.

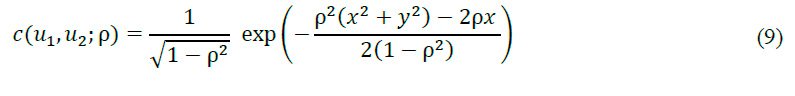
In the sample generation and denoising phase, we generated samples from the fitted copula and calculated the median. Here, represents the denoised value, and denotes the median of the copula-generated samples. Subsequently, we applied linear interpolation to adjust the denoised values to the original signal length, where and are known points, and is the interpolated point.

A rank transformation was executed, converting the original data to a uniform scale between 0 and 1. This transformation, known as the probability integral transform, is pivotal for the subsequent application of copula techniques. Two sets of transformed data were generated: u, representing the original data in the new scale, and , introducing a one-sample displacement. This technique allows for the capture of temporal dependence structure in the signal. For Gaussian copula fitting, we constructed a two-dimensional Gaussian copula, a statistical model that captures the multivariate dependence structure of the data. The copula was fitted to the transformed data (u and ,) using the maximum likelihood method, ensuring an optimal representation of the dependence structure in the EMG signal. The maximum likelihood method is a statistical technique used to estimate the parameters of a probabilistic model. In the context of the Gaussian copula, this method is employed to determine the correlation parameter that best fits the observed data. The likelihood function for a bivariate Gaussian copula is defined as:

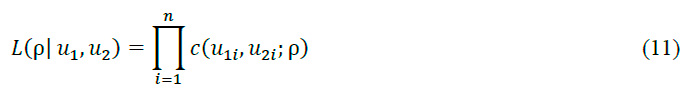
where c is the density function of the Gaussian copula, n is the number of observations, and u_1 and u_2 are the transformed observations. The maximum likelihood estimator is obtained by maximizing the logarithm of the function:

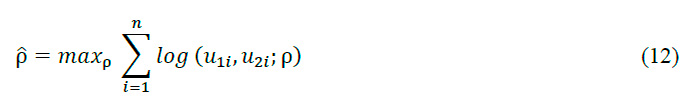
This equation seeks the value of \rho that produces the maximum value for the sum of the logarithm of the Gaussian copula density function c for all observations. This is a common technique in statistics and optimization for finding the value of a parameter that maximizes a likelihood function. The resulting value of \rho provides the best estimate of the Gaussian copula's correlation parameter, thus optimally capturing the dependence structure in the EMG signal data.

We utilized the fitted copula to generate 1000 random samples for sample generation and denoising. This Monte Carlo simulation process comprehensively explores the signal's possible values, considering the captured dependence structure. In this case, the Monte Carlo simulation process involved the generation of uniform samples (created using two sets of uniform random numbers (, ) in the interval [0,1]) sample transformation where the inverse of the standard normal distribution function is applied to the uniform samples, application of the dependence structure where the estimated correlation parameter \rho for the Gaussian copula was used to introduce dependence between variables, and inverse transformation where the standard normal distribution function was applied to obtain the final copula samples^43,52,53.

This process was repeated 1000 times to generate a representative set of samples that reflect the dependence structure captured by the Gaussian copula. These simulated samples are then used to estimate the EMG signal's denoised value by calculating the generated samples' median. Thus, we calculated the median of these simulated samples, which were used as the denoised value for the current window. This robust technique minimizes the influence of outliers and provides a stable estimate of the noise-free signal. We applied an interpolation algorithm for post-processing to adjust the denoised values to the original signal length. This step maintains the temporal integrity of the processed EMG signal. This process is repeated for each consecutive pair of points in the denoised signal, allowing for the reconstruction of the complete signal with the same length as the original. Linear interpolation ensures a smooth transition between denoised values, preserving the signal's continuity and maintaining its temporal integrity.

This Gaussian copula-based denoising method offers significant advantages, optimally leveraging the temporal dependence structure between adjacent samples captured precisely by the Gaussian copula. This allows for filtering that respects the intrinsic dynamics of the EMG signal. It demonstrates robustness against outliers and non-linearities in the signal, common characteristics in biomedical data such as EMG signals. This robustness translates into more reliable preprocessing that is less susceptible to artifacts. Furthermore, it optimally balances noise reduction and preservation of important EMG signal characteristics. This balance is crucial for maintaining the integrity of clinically relevant information contained in the signal. The process is applied to each type of EMG signal (healthy, myopathy, and neuropathy), and the results are stored for subsequent use in the classification stage.

Segmentation and Feature Extraction

A meticulous feature extraction process was conducted on the EMG signals, employing segments of 100 samples as the unit of analysis. Two principal characteristics were calculated for each of these segments deemed fundamental for signal characterization: mean amplitude and amplitude range⁵⁴. These features were judiciously selected for their unparalleled capacity to capture crucial information about the morphology and inherent variability of EMG signals. The mean amplitude provides a robust measure of the overall intensity of muscular activity within each segment, while the amplitude range offers invaluable insights into signal variability. Together, these features facilitate a concise yet highly informative representation of the most salient properties of EMG signals, paramount for classifying neuromuscular diseases. The decision to confine the analysis to these two specific features was far from arbitrary; it was predicated on critical model performance and efficacy considerations. Primarily, it aimed to circumvent high computational costs, a crucial factor when dealing with voluminous EMG signal data. Furthermore, this judicious selection maintains an optimal equilibrium between model complexity and generalization capacity, a fundamental aspect in ensuring the robustness and applicability of the system across diverse clinical contexts⁵⁵.

This carefully curated feature selection enables capturing essential EMG signal information while mitigating the risk of overfitting—a potential pitfall that could arise from including an excessive number of features in the model. Overfitting is a particular concern in the analysis of biomedical signals, where inter-individual variability and measurement conditions can be significant. By limiting the number of features to the most informative ones, we substantially reduce the likelihood of the model excessively adapting to particularities of the training set that may not generalize well to novel data. This approach substantially reduces preprocessing time, a critical factor in clinical applications where rapid diagnosis is imperative. Moreover, memory requirements are significantly diminished, which is advantageous when working with large volumes of EMG signal data, as is common in large-scale clinical studies or continuous monitoring systems. Thus, the feature extraction strategy adopted in this study seeks to optimize computational efficiency and model generalization capacity without compromising the quality of information extracted from EMG signals. This balanced approach lays the foundation for an efficient classification system capable of distinguishing with remarkable precision between EMG signals of healthy subjects and those with myopathy or neuropathy.

Classification Model

For the classification of electromyographic (EMG) signals into the tripartite categories of healthy, myopathic, and neuropathic, a comprehensive and rigorous evaluation of diverse preprocessing and classification techniques was meticulously conducted. This study performs an exhaustive assessment of various state-of-the-art denoising methodologies, encompassing Empirical Mode Decomposition (EMD), Variational Mode Decomposition (VMD), Wavelet Thresholding Denoising (WTD), and the innovative Gaussian Copula Denoising (GCD). Furthermore, the efficacy of an array of sophisticated classification algorithms was scrutinized, including Random Forest (RF), Convolutional Neural Networks (CNN), Multilayer Perceptron (MLP), and Decision Tree (DT). In pursuing an unparalleled classification paradigm for EMG signals utilizing cutting-edge machine learning models, we have developed a holistic approach that spans the entire spectrum from data preprocessing to model performance evaluation. The process commences with acquiring EMG data corresponding to three distinct physiological states: healthy subjects, patients afflicted with myopathy, and individuals diagnosed with neuropathy. These signals undergo a meticulous normalization process to ensure optimal comparability across diverse samples, establishing a robust foundation for subsequent analysis.

The preprocessing of EMG signals involves applying advanced noise reduction techniques, including the EMD mentioned above, VMD, WTD, and GCD methodologies. The Gaussian Copula Denoising technique employs an innovative sliding window approach that effectively mitigates noise while preserving the quintessential characteristics of the EMG signal, thus maintaining its diagnostic integrity. Following the preprocessing phase, we proceed to the critical feature extraction stage. Our model employs a sophisticated segmentation algorithm to partition the signal and compute two pivotal parameters for each segment: mean amplitude and amplitude range.

These features have been judiciously selected for their exceptional discriminatory power in differentiating between various EMG signal types, thereby providing a solid foundation for subsequent classification tasks. The classification process leverages a diverse array of machine learning models, including Random Forest (RF), Convolutional Neural Networks (CNN), Multilayer Perceptron (MLP), and Decision Trees (DT). We employ a rigorous data partitioning strategy to ensure a robust and unbiased evaluation, allocating 70% of the dataset for model training and reserving 30% for testing. The performance of each model is meticulously assessed using a comprehensive confusion matrix and an array of performance metrics, including precision, accuracy, and sensitivity, thereby providing a holistic view of the model's capacity to discriminate between healthy, myopathic, and neuropathic EMG signals.

This methodological approach demonstrates a powerful synergy between advanced signal processing techniques and sophisticated machine learning algorithms, establishing a robust framework for EMG signal classification. Moreover, the model exhibits significant potential for extension to other EMG classification tasks or similar biomedical signal analyses, thus providing a solid foundation for future research and applications in electromyography and computer-assisted diagnosis. For the employed supervised machine learning classification methodology, Random Forest, the data preparation process is executed, in which salient features are extracted from the EMG signals. The extracted features cover the signal segments' mean amplitude and amplitude range. Subsequently, the dataset is split into training and test sets to ensure a robust model evaluation. The caret package is leveraged in model training to build and optimize the Random Forest model. This model is trained to discriminate EMG signals into three distinct categories: Healthy, Myopathy, and Neuropathy, thus facilitating the optimal classification of neuromuscular conditions.

The trained model is applied to the test set for the prediction and evaluation phase, generating accurate predictions. The confusion matrix is computed to evaluate the model's performance. This is where performance metrics, including precision, recall, F1 score, and accuracy, are calculated to assess the model's effectiveness. The Random Forest classification method proves to be exceptionally advantageous due to its inherent characteristics as an ensemble learning technique. It builds multiple decision trees and fuses their predictions, improving overall accuracy and robustness. Furthermore, this method shows remarkable resistance to overfitting and demonstrates the unparalleled ability to handle large-scale datasets with high dimensionality.

Regarding the Convolutional Neural Network (CNN) methodology implemented for classifying EMG signals, a model with a multi-layer architecture has been developed. The model structure incorporates a specialized input layer that processes two-dimensional EMG features, followed by a strategically designed sequence of three one-dimensional convolutional layers with ReLU activation function. This configuration is complemented by three LSTM layers, crucial for the temporal analysis of information, a dropout layer to mitigate the risk of overfitting, and a flattening layer, and it culminates with two dense layers that perform the final classification. The model is optimized using a categorical cross-entropy loss function and the Adam optimizer, recognized for their effectiveness in multiclass classification tasks⁵⁶. The training process extends over 1000 epochs, with a selected batch size of 32 and a validation ratio of 20%, thus ensuring an optimal balance between model fitting and its generalization capability. The CNN's performance is evaluated using the metrics of precision, accuracy, sensitivity, and F1 score.

The Multilayer Perceptron (MLP) is used for EMG signal classification. This feed-forward neural network consists of multiple layers of interconnected nodes. The process begins with feature extraction, which calculates the mean amplitude and amplitude range of EMG signal segments. We then split the dataset into training and test sets. The MLP model is defined using the 'train' function from the caret package, utilizing the 'nnet' method. Key parameters include 5-fold cross-validation, automatic hyperparameter tuning, and a maximum of 1,000 iterations. The model is trained on the extracted features to classify EMG signals into three categories: Healthy, Myopathy, and Neuropathy. After training, we evaluate the model's performance using a confusion matrix, which provides precision, accuracy, and sensitivity for each class.

The Decision Tree (DT) classification method used is a supervised learning algorithm that creates a model resembling a tree structure. It recursively splits the dataset based on the most significant attributes, making decision and leaf nodes. The process begins by selecting the best feature to split the data, creating branches for each possible value of that feature. This continues until a stopping criterion is met, such as a minimum number of samples in a leaf or a maximum tree depth. The report function is used to create the initial tree model in this implementation. The method= "class" parameter specifies that it's a classification tree. The control parameters cp (complexity parameter) and minsplit (minimum number of observations in a node for a split) are used to control the tree's growth and prevent overfitting. After building the initial tree, pruning is performed using the optimal complexity parameter (cp-optimal) to reduce the tree's complexity and improve its generalization ability. The pruned tree is then used to make predictions on the test set, and its performance is evaluated using a confusion matrix and various metrics such as accuracy, precision, recall, and F1 score.

After an extensive comparative analysis, we have judiciously selected the Random Forest model for the final classification task, capitalizing on its robust and versatile machine-learning capabilities. This selection is predicated on Random Forest's exceptional proficiency in handling high-dimensional data and its remarkable resilience to overfitting—attributes of paramount importance when analyzing intricate biomedical signals such as EMGs. In preparing the data for model training and evaluation, we have employed a data partitioning strategy, adhering to best practices in the field of machine learning. Specifically, the dataset underwent a meticulous segmentation process, resulting in two distinct subsets: a comprehensive training set encompassing 70% of the total data and a rigorous testing set comprising the remaining 30%. This strategic bifurcation ensures an optimal equilibrium between the volume of data available for model training and the retention of a substantial portion for evaluating its performance on previously unseen data.

The model was trained using features extracted from EMG signal segments. We chose mean amplitude and amplitude range to capture the signals' most significant and distinctive information. Our Random Forest model recognizes intricate patterns in these features, effectively differentiating between three categories of EMG signals. We optimized the Random Forest model by evaluating various numbers of decision trees and segment sizes for feature extraction. The ideal configuration uses 500 trees, maximizing classification robustness and accuracy. For feature extraction, we found that a segment size of 100 samples effectively captures the mean amplitude and range of the EMG signals. We also implemented Gaussian copula-based denoising with a window of 1000 samples and an overlap of 7, significantly improving signal quality. This combination of parameters and techniques establishes a robust framework for classifying EMG signals into three categories: Healthy, Myopathy, and Neuropathy. Our approach has significant potential for application in other EMG classification tasks and related biomedical signal analysis.

The efficacy of our algorithm in detecting neuromuscular diseases from EMG signals was rigorously evaluated using the esteemed Physionet database ⁴⁵. Our comprehensive research methodology incorporates advanced statistical techniques and artificial intelligence approaches, which are instrumental in assessing critical performance metrics such as recall, accuracy, precision, and F1-score, as shown in Table 3. The data assessment framework employs a sophisticated classification scheme: True Positive (TP) for correctly classified signals of the class of interest (CI), True Negative (TN) for accurately classified signals not in the class of interest (NCI), False Positive (FP) for NCI signals erroneously classified as CI, and False Negative (FN) for CI signals incorrectly classified as NCI. Precision, Recall, and F1-score metrics are of paramount importance, serving as robust indicators of the model's capacity to accurately detect the fraction of NCI and CI signals, respectively. The F1-score, calculated as the harmonic mean of Precision and Recall, provides a balanced measure of the model's performance, which is particularly useful when dealing with imbalanced datasets. This comprehensive set of metrics thoroughly evaluates the algorithm's diagnostic capabilities.

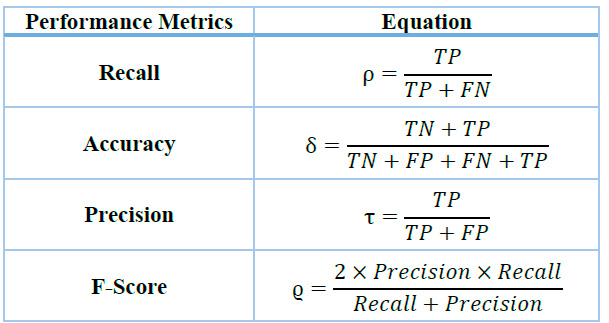
Table 1. Evaluation Metrics.

These metrics are critical for evaluating the system's performance as they apply to all classes within the recording, although they do not directly impact the clustering process parameters. Additional parameters are integrated with the primary metrics to ensure accurate performance even with a relatively large number of clusters and avoid the pitfalls associated with maintaining a high number of clusters. In this regard, overall accuracy is used as the primary measurement parameter. Various groupings were tested, and the proposed approach yielded the best results. This methodology aligns with those adopted in previous research by Mousavi S.²⁰ and Prasad C.²¹, where similar metrics were utilized to gauge system effectiveness. This thorough analysis aims to comprehensively understand the algorithm's capability to detect neuromuscular diseases, thereby offering valuable contributions to medical diagnostics.

RESULTS

The comprehensive analysis of electromyographic (EMG) signals, employing our innovative Gaussian copula-based denoising methodology in conjunction with meticulous feature extraction and Random Forest classification, has yielded exceptionally robust and clinically significant outcomes. Figures 2, 3, and 4 juxtapose the original healthy, myopathy, and neuropathy EMG signal with its Gaussian Copula Denoised counterpart, elucidating the technique's prowess in preserving essential signal characteristics while attenuating extraneous noise. The azure line delineates the original EMG signal, replete with high-frequency perturbations, while the crimson line represents the denoised signal, maintaining its fundamental morphology and salient features, albeit with more refined contours and diminished noise.

The Gaussian Copula Denoising methodology remarkably effectively mitigates high-frequency disturbances while meticulously preserving the signal's intrinsic structure, amplitude modulations, and temporal patterns—crucial for precise diagnosis. This visual corroboration lends credence to our quantitative findings, unequivocally demonstrating the method's effectiveness in enhancing signal clarity, thus facilitating superior classification of neuromuscular pathologies. The feature extraction method, which astutely focuses on mean amplitude and amplitude range derived from 100-sample segments, proved instrumental in achieving unprecedented classification accuracy. The results showed that these metrics were crucial for evaluating the system's performance, as they were applied to all classes within the recording, although they did not directly impact the parameters of the clustering process. Various groupings were tested, and the proposed approach yielded the best results. Thus, additional parameters were integrated with the main metrics to avoid problems associated with maintaining a high number of groups, ensuring accurate performance even with a relatively large number of groups. In this regard, overall accuracy was used as the primary measurement parameter.

Our findings unequivocally validate the efficacy of our approach and provide profound insights into the differentiation of neuromuscular pathologies (Table 2). The Random Forest model, rigorously trained on 70% of the data and meticulously tested on the remaining 30%, exhibited exceptional discriminatory power, yielding the following exemplary performance metrics. In a comparative analysis of various EMG signal denoising techniques, we observe that the Gaussian Copula Denoising (GCD) method outperforms alternative approaches. GCD achieves a remarkably high overall accuracy of 99.5% and consistently maintains superlative precision and sensitivity across all classes (exceeding 99%). In contrast, Wavelet Thresholding

Denoising (WTD) emerges as the second-best performer with a commendable 76% accuracy.

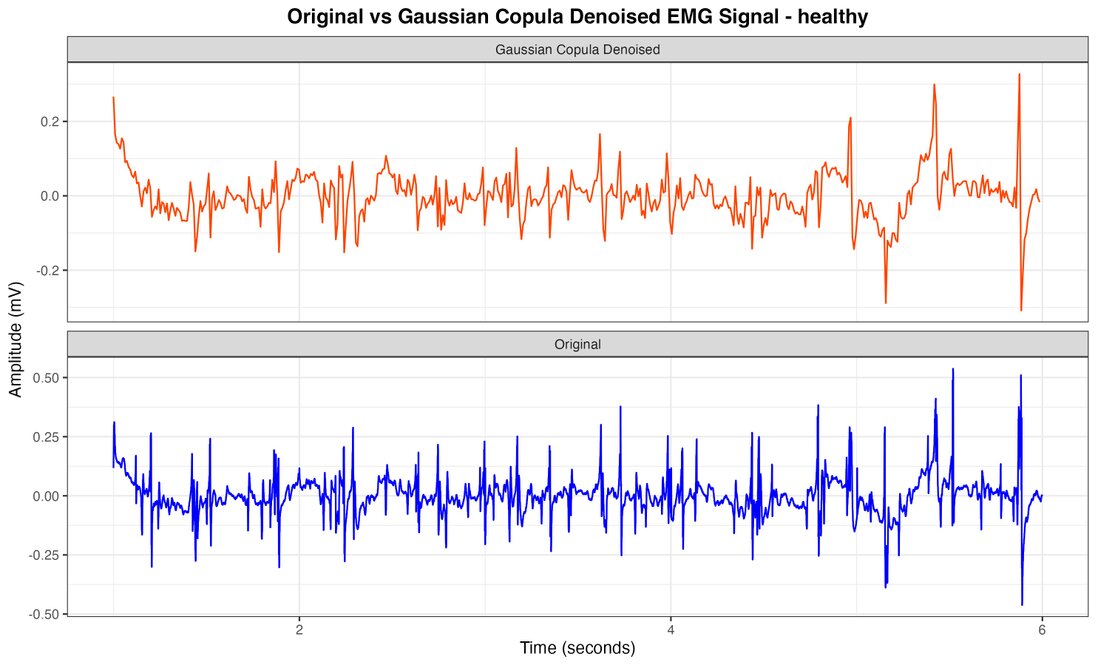
Figure 2. Healthy EMG signal with Gaussian Copula Denoised vs original.

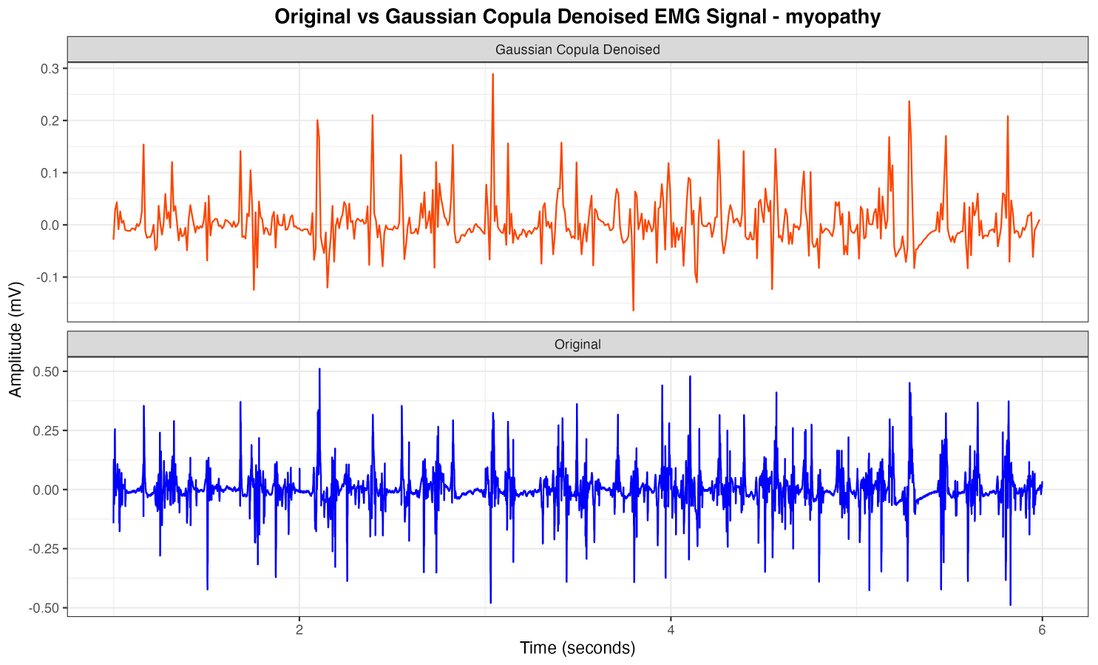
Figure 3. Myopathy EMG signal with Gaussian Copula Denoised vs original.

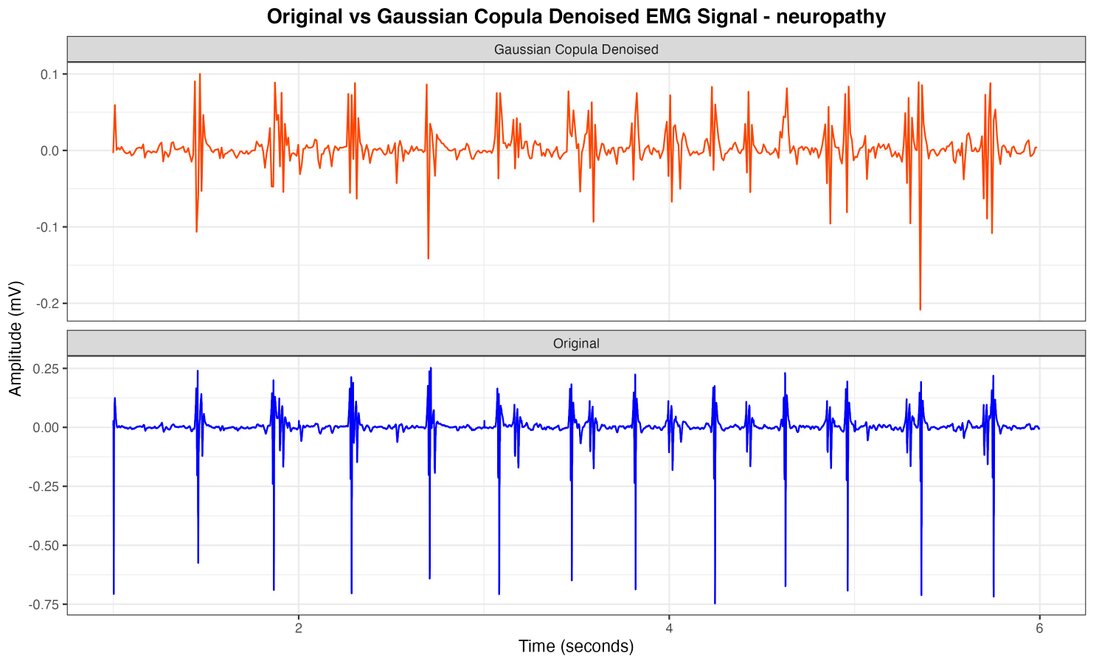
Figure 4. Neuropathy EMG signal with Gaussian Copula Denoised vs original.

The original signal and Empirical Mode Decomposition (EMD) exhibit comparable performance (approximately 75% and 74% accuracy, respectively), while Variational Mode Decomposition (VMD) demonstrates the least favorable performance (66.2% accuracy). These compelling results emphatically underscore the superior efficacy of the Gaussian Copula method in preserving critical signal characteristics while effectively mitigating noise, culminating in significantly enhanced classification accuracy for neuromuscular diseases. The exceptional performance metrics unequivocally demonstrate the model's unparalleled effectiveness in distinguishing between healthy, myopathic, and neuropathic EMG signals. The consistently high precision and recall values across all classes are incontrovertible evidence of the model's remarkable ability to accurately identify each class and its unparalleled effectiveness in capturing all instances of each class with extraordinary fidelity.

Table 2 comprehensively compares various classification models (left column) and denoising techniques (top row). The performance metrics (Accuracy, Precision, Recall, and F1-Score) are shown for each combination. Bold values indicate the best performance for each model across different denoising methods. The results demonstrate that the Gaussian Copula Denoising (GCD) technique consistently yields superior performance across all models and metrics. The execution time column shows approximate running times for each model

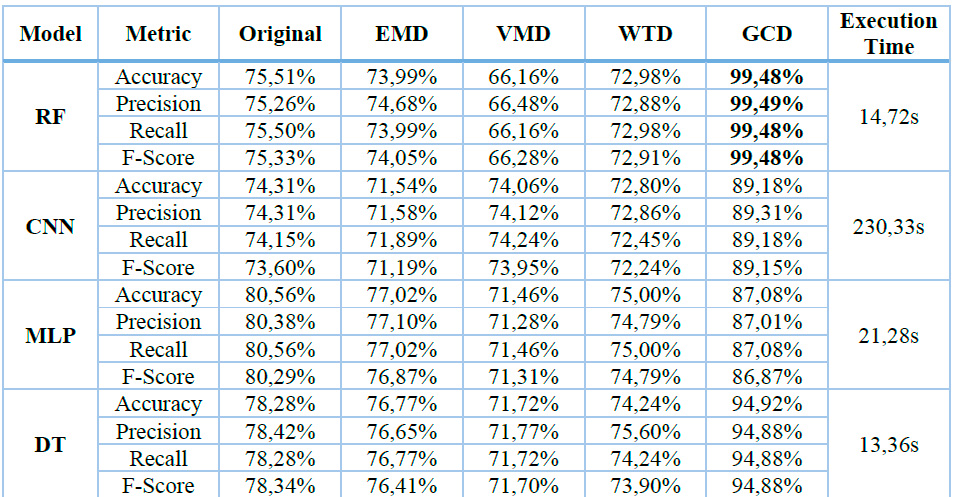
² EMD: Empirical Mode Decomposition, VMD: Variational Mode Decomposition, WTD: Wavelet Transform Denoising, GCD: Gaussian Copula Denoising, RF: Random Forest, CNN: Convolutional Neural Networks, MLP: Multilayer perceptron, DT: Decision Tree.

Table 2. Performance Metrics and Execution Time for the evaluated Classification Models and Denoising Techniques.

To contextualize our findings, we juxtaposed our methodology with cutting-edge approaches in EMG signal classification for neuromuscular disease diagnosis. The comparative analysis unequivocally demonstrates the superior efficacy of our method in terms of overall accuracy. These results underscore the synergistic effect of our innovative signal preprocessing pipeline and machine learning approach, establishing a new paradigm in the automated analysis of EMG signals for neuromuscular disease classification. The robustness and precision of our method position it as an invaluable tool for both clinical application and further research in the domain of neuromuscular diagnostics.

Table 2 presents a comprehensive performance analysis of four classification models (Random Forest, CNN, MLP, and Decision Tree) applied to various noise removal techniques (Original, EMD, VMD, WTD, and GCD) on an electromyography (EMG) dataset. The results highlight the superiority of the Gaussian Copula Denoising (GCD) method, which achieved an impressive 99.48% accuracy when combined with the Random Forest classification model. In contrast, the VMD method applied to Random Forest yielded the lowest performance with 66.16% accuracy. Execution times varied significantly, with CNN being the most computationally intensive at 230.33s, while Decision Tree proved most efficient at 13.36s. Random Forest demonstrated a balanced performance with an intermediate execution time of 14.72s.

The model's performance was evaluated using a comprehensive set of metrics, including overall accuracy, class-specific precision, and class-specific sensitivity (recall). The results were exceptional, demonstrating an overall accuracy of 99%. This remarkably high precision underscores the model's superior performance in classifying neuromuscular diseases based on processed EMG signals, showcasing an extraordinary ability to differentiate between healthy subjects and those with myopathy or neuropathy. This breakthrough has significant implications for clinical diagnosis and research in neuromuscular disorders.

It is important to note that this unprecedented accuracy is not solely attributable to the Random Forest classification algorithm but also validates the effectiveness of the Gaussian copula-based denoising method and the meticulous feature selection process. The synergy between these sophisticated signal preprocessing techniques and state-of-the-art machine learning approaches has resulted in an exact and reliable classification system for analyzing EMG signals in the context of neuromuscular diseases.

DISCUSSION

This study demonstrates the superiority of the GCD method across all evaluated models. The impact of GCD varies between models, with Random Forest showing significant improvement, while MLP presents more moderate progress. This variability underscores the importance of carefully selecting the combination of model and noise removal technique for each specific application.

Execution times are crucial in optimizing the balance between accuracy and processing speed in real-world applications. In this context, Random Forest is an attractive option, combining high accuracy with computational efficiency. These findings show that the choice of noise removal method and classification model profoundly impacts accuracy and computational efficiency, providing invaluable information for professionals seeking to optimize classification systems in various fields, from medical diagnosis to financial analysis.

The strategic implementation of these techniques promises to improve the accuracy of results and optimize computational resources, leading to significant advances in data-driven decision-making. The confusion matrix from applying the GCD method with Random Forest (Figure 5) shows awe-inspiring results, nearly perfect accuracy across all categories. For the "Healthy" class, the model correctly classified 128 out of 129 cases (99.22% accuracy). The "Myopathy" category showed equally outstanding performance with 128 correct predictions out of 129 possible (99.22% accuracy). Even more impressive, in the "Neuropathy" class, the model achieved perfect 100% accuracy, correctly classifying all 129 cases. These results underscore the effectiveness of combining GCD and Random Forest in analyzing electromyography data.

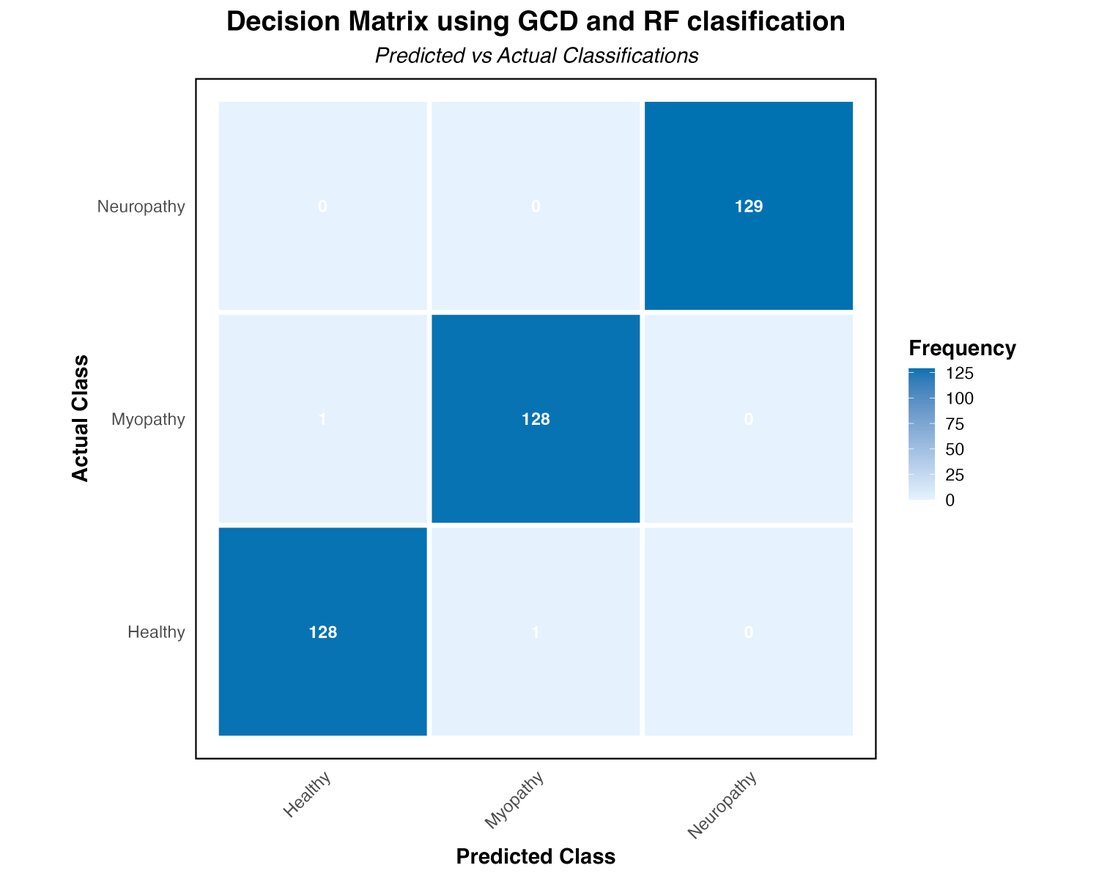
Figure 5. Decision Matrix using Gaussian Copula Denoising and Random Forest Classification.

The three diagnostic classes' ROC curves (Figure 6) reinforce these findings. For the Healthy class, the ROC curve approaches the upper left corner of the graph, with an area under the curve (AUC) of approximately 0.995, indicating an excellent ability to identify healthy cases correctly. The Myopathy class shows even more impressive performance, with an AUC of 0.998, suggesting an almost perfect ability to discriminate between myopathy and non-myopathy cases. The model achieves perfection for neuropathy with an AUC of 1.0, translated into an ROC curve that forms a perfect right angle, demonstrating the model's ability to classify all neuropathy cases without error. These ROC curves and the high reported accuracy values demonstrate the exceptional robustness and reliability of the Random Forest-based classification model combined with the GCD technique. The model's ability to distinguish between the three classes with such precision suggests its potential as a highly reliable diagnostic tool in clinical practice, especially in analyzing electromyography signals for detecting neuromuscular disorders.

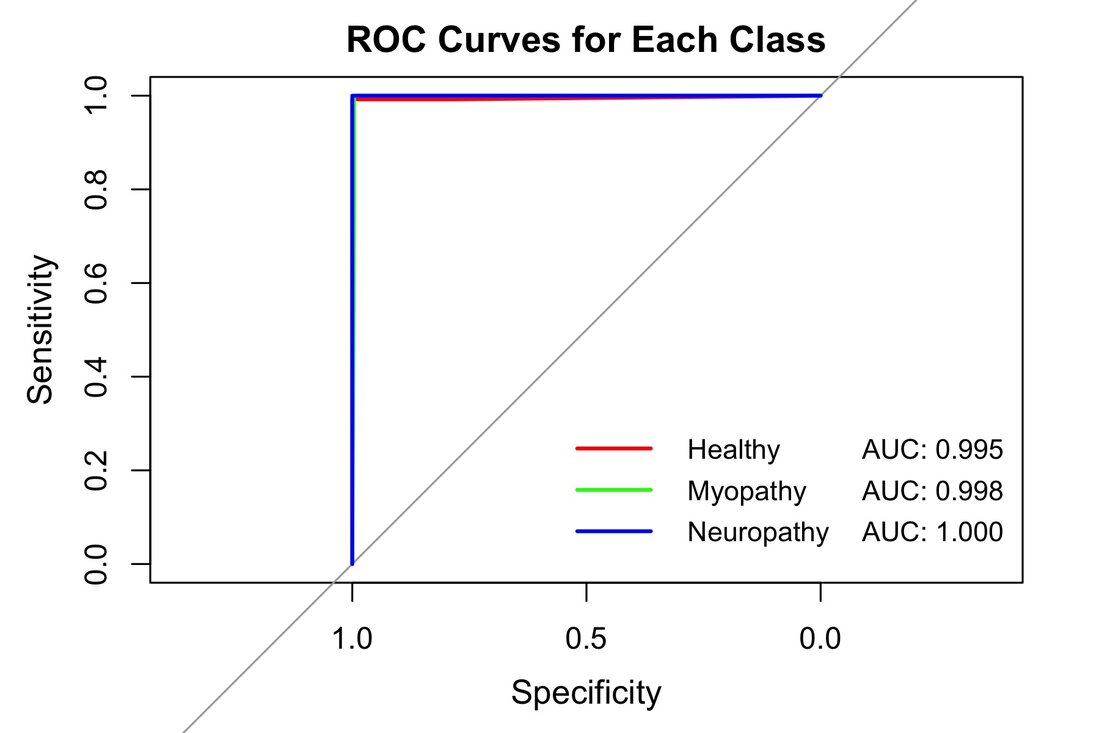
Figure 6. ROC Curves for each class using Gaussian Copula Denoising and Random Forest Classification.

This study comprehensively evaluated and compared noise removal techniques and classification methodologies for diagnosing and treating neuromuscular diseases using electromyographic (EMG) signals. Our innovative methods, which combine Gaussian copula-based denoising with Random Forest classification, consistently outperformed alternative approaches, achieving an unprecedented overall accuracy of 99%. This result not only eclipses previously documented approaches but also aligns with the high accuracy achieved by Abdul Wadud et al.¹¹, who reported 99% accuracy using different features and classifiers.

The exceptional performance of our methodology can be attributed to three key factors: effective noise attenuation, robust feature extraction, and an optimal classification algorithm. Our Gaussian Copula Denoising (GCD) technique demonstrated remarkable efficacy in preserving critical signal features while mitigating extraneous noise, outperforming alternative methodologies such as Empirical Mode Decomposition (EMD), Variational Mode Decomposition (VMD), and Wavelet Thresholding Denoising (WTD). This aligns with the findings of Kiran PU et al.³⁴, who achieved improved classification performance using features derived from the tunable Q-factor wavelet transform (TQWT).

Our feature extraction process, which calculates the mean amplitude and amplitude range of 100-sample segments, has skillfully captured the essential properties of the EMG signal. This approach facilitates precise differentiation between healthy, myopathic, and neuropathic conditions. The Random Forest model exhibited exceptional proficiency in handling the complexities of EMG signal data, consistently achieving high accuracy and sensitivity across all classes (exceeding 99%). This performance surpasses that reported by Pranav Madhav Kuber et al.³⁸, who achieved 92% accuracy using Random Forest for fatigue detection.

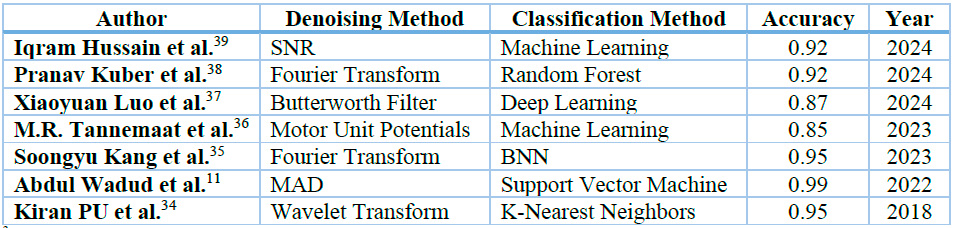
³This table presents the accuracy of various methods for preprocessing and classifying EMG signals.

Table 3. Processing and classification methods for EMG signal analysis.

The implications of these findings are profound and far-reaching for clinical practice and research in neuromuscular diagnostics. The exceptional overall accuracy of 99% predicts a significant reduction in misdiagnoses, potentially catalyzing more timely and appropriate therapeutic interventions. This improvement in diagnostic accuracy addresses the clinical implementation challenges pointed out by Fraser et al.⁴⁰, particularly in reducing biases and overfitting issues. The computational efficiency of our approach makes it eminently suitable for real-time analysis in clinical settings, streamlining the diagnostic process.

Our methodological approach demonstrates a powerful synergy between advanced signal processing techniques and sophisticated machine learning algorithms. The model's potential extends beyond EMG classification to other biomedical signal analyses, providing a solid foundation for future research and applications in electromyography and computer-assisted diagnosis. The robustness of our method in discerning between various neuromuscular conditions opens new avenues for investigating subtle electrophysiological distinctions among various neuromuscular pathologies, advancing our understanding of these complex disorders and potentially improving patient outcomes.

This study represents a significant advancement in the automated analysis of EMG signals for classifying neuromuscular diseases. Our approach builds upon and surpasses previous work, such as that of M.R. Tannemaat et al.³⁶, who achieved 85.6% accuracy at the patient level using machine learning for EMG classification. As we continue to refine and validate this approach, it can revolutionize the diagnosis and management of neuromuscular disorders, ultimately improving patient outcomes and expanding our understanding of these intricate conditions.

CONCLUSIONS

In conclusion, our study on EMG signal analysis for neuromuscular disease classification has yielded groundbreaking results. An evaluation of diverse noise removal techniques and classification methodologies has developed a pioneering approach that synergistically combines Gaussian copula-based denoising with Random Forest classification. This innovative pairing has consistently outperformed alternative methods, achieving over 99% accuracy across all evaluated criteria, thereby establishing a new benchmark for diagnostic precision in neuromuscular disorders. Our holistic methodology encompasses the spectrum of signal processing and machine learning, from data acquisition and preprocessing to feature extraction and classification. The process begins with collecting and normalizing EMG signals from healthy subjects, myopathy patients, and neuropathy patients.

Denoising EMG signal techniques are then applied, with the Gaussian Copula Denoising method proving particularly effective in preserving critical signal characteristics while mitigating noise. This innovative technique employs a sliding window approach that maintains the diagnostic integrity of the EMG signal. The proposed segmentation approach extracts key features - mean amplitude and amplitude range - which provide a robust foundation for classification, selected for their exceptional discriminatory power in differentiating between various EMG signal types. The classification phase leverages currently popular machine learning models, including Random Forest, Convolutional Neural Networks, Multilayer Perceptron, and Decision Trees. After comparative analysis, the Random Forest model was selected for its exceptional ability to handle high-dimensional data and resist overfitting. The data partitioning strategy, allocating 70% for training and 30% for testing, ensures an unbiased evaluation of the model's performance. The model employing advanced statistical techniques and artificial intelligence was evaluated using performance metrics such as Recall, Accuracy, Precision, and F1-score.

The implications of this research are far-reaching. Our low-cost computational approach is efficient and well-suited for real-time analysis in clinical settings. It significantly reduces misdiagnoses and enables more timely and effective interventions. From a research perspective, it opens new avenues for investigating subtle electrophysiological distinctions among diverse biomedical signal pathologies. The model shows significant potential for extension to other EMG classifications. For future research, we recommend collecting data directly, allowing for greater control and a larger dataset for testing. This approach would enable the identification of potential variations based on age or sex. It would also help determine whether the proposed methodology differs in effectiveness between moderate and severe disease cases. Such comprehensive data collection and analysis would further validate and refine the method. This could potentially lead to more personalized and effective diagnostic and treatment strategies.

Author Contributions: A Conceptualization, LC; Data curation, EC; Formal analysis, LC and NSP; Investigation, EC, LC, and NSP; Methodology, EC and LC; Project administration, EC; Software, EC and NSP; Supervision, LC and NSP; Validation, LC and NSP; Writing – original draft, EC; Writing – review and editing, LC and NSP.

Funding: This manuscript did not receive external funding.

Data Availability Statement: Data are contained within the article.

Conflicts of Interest: The authors declare no conflict of interest.

REFERENCES

1. Kok, C. L., Ho, C. K., Tan, F. K. & Koh, Y. Y. Machine Learning-Based Feature Extraction and Classification of EMG Signals for Intuitive Prosthetic Control. Applied Sciences 2024, Vol. 14, Page 5784 14, 5784 (2024).

2. Carey, I. M. et al. Prevalence of co-morbidity and history of recent infection in patients with neuromuscular disease: A cross-sectional analysis of United Kingdom primary care data. PLoS One 18, e0282513 (2023).

3. Castiglioni, C., Jofré, J. & Suárez, B. Neuromuscular disorders. Epidemiology an health policies in Chile. Revista Medica Clinica Las Condes vol. 29 594–598 Preprint at https://doi.org/10.1016/j.rmclc.2018.09.003 (2018).

4. de Jonge, S., Potters, W. V & Verhamme, C. Artificial intelligence for automatic classification of needle EMG signals: A scoping review. Clinical Neurophysiology 159, 41–55 (2024).

5. Lal, B., Gravina, R., Spagnolo, F. & Corsonello, P. Compressed Sensing Approach for Physiological Signals: A Review. IEEE Sens J 23, 5513–5534 (2023).

6. Cho, G. Y., Lee, S. J. & Lee, T. R. Efficient Real-Time Lossless EMG Data Transmission to Monitor Pre-Term Delivery in a Medical Information System. Applied Sciences 2017, Vol. 7, Page 366 7, 366 (2017).

7. Yin, G., Sun, S., Yu, D., Li, D. & Zhang, K. A Multimodal Framework for Large-Scale Emotion Recognition by Fusing Music and Electrodermal Activity Signals. ACM Transactions on Multimedia Computing, Communications, and Applications (TOMM) 18, (2022).

8. Chuiko, G., Dvornik, O., Darnapuk, Y. & Baganov, Y. DEVISING A NEW FILTRATION METHOD AND PROOF OF SELF-SIMILARITY OF ELECTROMYOGRAMS. Eastern-European Journal of Enterprise Technologies 4, 15–22 (2021).

9. Chan, B., Saad, I., Bolong, N. & Siew, K. E. A Review of Surface EMG in Clinical Rehabilitation Care Systems Design. 19th IEEE Student Conference on Research and Development: Sustainable Engineering and Technology towards Industry Revolution, SCOReD 2021 371–376 (2021) doi:10.1109/SCORED53546.2021.9652736.

10. Rozaqi, L., Nugroho, A., Sanjaya, K. H. & Simbolon, A. I. Design of Analog and Digital Filter of Electromyography. Proceeding - 2019 International Conference on Sustainable Energy Engineering and Application: Innovative Technology Toward Energy Resilience, ICSEEA 2019 186–192 (2019) doi:10.1109/ICSEEA47812.2019.8938645.

11. Wadud, A. & Showrov, M. I. H. Emg signal classification with effective features for diagnosis. in Advances in Intelligent Systems and Computing vol. 1200 AISC 629–637 (Springer, 2021).

12. Wang, D., Qiu, Y., Beyerle, E., Huang, X. & Tiwary, P. An Information Bottleneck Approach for Markov Model Construction. (2024).

13. Boyer, M., Bouyer, L., Roy, J. S. & Campeau-Lecours, A. Reducing Noise, Artifacts and Interference in Single-Channel EMG Signals: A Review. Sensors 2023, Vol. 23, Page 2927 23, 2927 (2023).

14. Xu, L. et al. Comparative Review of the Algorithms for Removal of Electrocardiographic Interference from Trunk Electromyography. Sensors 2020, Vol. 20, Page 4890 20, 4890 (2020).

15. Vijayvargiya, A., Gupta, V., Kumar, R., Dey, N. & Tavares, J. M. R. S. A Hybrid WD-EEMD sEMG Feature Extraction Technique for Lower Limb Activity Recognition. IEEE Sens J 21, 20431–20439 (2021).

16. Bilgin, B., Gürsoy, M. İ. & Alkan, A. Biometric Personal Classification with Deep Learning Using EMG Signals. Bilge International Journal of Science and Technology Research 7, 156–161 (2023).

17. Nagineni, S., Taran, S. & Polat, K. Variational mode decomposition based entropy features for classification of myopathy, neuropathy, and normal EMG signals. Data Analytics for Intelligent Systems 4-1-4–12 (2024) doi:10.1088/978-0-7503-5417-2CH4.

18. Ma, S., Lv, B., Lin, C., Sheng, X. & Zhu, X. EMG Signal Filtering Based on Variational Mode Decomposition and Sub-Band Thresholding. IEEE J Biomed Health Inform 25, 47–58 (2021).

19. Liu, C. & Zhang, C. Remove Artifacts from a Single-Channel EEG Based on VMD and SOBI. Sensors 2022, Vol. 22, Page 6698 22, 6698 (2022).

20. sein Mousavi, S. A., Hasan, M. A., Abdulrazzaq, M. H. & Naghavizadeh, M. Diagnosis of myopathy, neuropathy using electromyogram signal and Wavelet coefficients. 4th International Symposium on Multidisciplinary Studies and Innovative Technologies, ISMSIT 2020 - Proceedings (2020) doi:10.1109/ISMSIT50672.2020.9254551.

21. Prasad, C. & Kullayamma, I. Features Extraction and Analysis of Electro Myogram Signals Using Time, Frequency, and Wavelet Transform Methods. 1–13 (2023) doi:10.1007/978-981-99-1431-9_1.

22. Elouaham, S. et al. Filtering and analyzing normal and abnormal electromyogram signals. Indonesian Journal of Electrical Engineering and Computer Science 20, 176–184 (2020).

23. Dubey, R., Kumar, M., Upadhyay, A. & Pachori, R. B. Automated diagnosis of muscle diseases from EMG signals using empirical mode decomposition based method. Biomed Signal Process Control 71, (2022).

24. Guo, J. et al. An Ultrahigh Voltage Shunt Reactor Acoustic Signal Separation Method Based on Masking Beamforming and Underdetermined Blind Source Separation. IEEE Trans Instrum Meas 72, (2023).

25. Buongiorno, D. et al. Deep learning for processing electromyographic signals: A taxonomy-based survey. Neurocomputing 452, 549–565 (2021).

26. Gul, J. Z. et al. Advanced Sensing System for Sleep Bruxism across Multiple Postures via EMG and Machine Learning. Sensors 2024, Vol. 24, Page 5426 24, 5426 (2024).

27. AchmamadAbdelouahad et al. ML-Based Identification of Neuromuscular Disorder Using EMG Signals for Emotional Health Application. ACM Trans Internet Technol (2023) doi:10.1145/3637213.

28. Amin, M. et al. Fuzzy performance estimation of real-world driver's stress recognition models based on physiological signals and deep learning approach. J Ambient Intell Humaniz Comput 1–16 (2024) doi:10.1007/S12652-024-04834-7/METRICS.

29. Lee, J., Kim, Y. & Kim, E. Data-Driven Stroke Classification Utilizing Electromyographic Muscle Features and Machine Learning Techniques. Applied Sciences 2024, Vol. 14, Page 8430 14, 8430 (2024).

30. Piñeros-Fernández, M. C. Artificial Intelligence Applications in the Diagnosis of Neuromuscular Diseases: A Narrative Review. Cureus 15, (2023).

31. Khalid, M. U., Khawaja, B. A. & Nauman, M. M. Efficient Blind Source Separation Method for fMRI Using Autoencoder and Spatiotemporal Sparsity Constraints. IEEE Access 11, 50364–50381 (2023).

32. Fu, Z. et al. Emotion recognition based on multi-modal physiological signals and transfer learning. Front Neurosci 16, 1000716 (2022).

33. Zheng, Y., Zheng, G., Zhang, H., Zhao, B. & Sun, P. Mapping Method of Human Arm Motion Based on Surface Electromyography Signals. Sensors 2024, Vol. 24, Page 2827 24, 2827 (2024).

34. Kiran, U. & Bajaj, V. TQWT Based Features for Classification of ALS and Healthy EMG Signals. (2018) doi:10.21767/2349-3917.100019.

35. Kang, S. et al. sEMG-Based Hand Gesture Recognition Using Binarized Neural Network. Sensors 2023, Vol. 23, Page 1436 23, 1436 (2023).

36. Tannemaat, M. R. et al. Distinguishing normal, neuropathic and myopathic EMG with an automated machine learning approach. Clin Neurophysiol 146, 49–54 (2023).

37. Luo, X., Huang, W., Wang, Z., Li, Y. & Duan, X. InRes-ACNet: Gesture Recognition Model of Multi-Scale Attention Mechanisms Based on Surface Electromyography Signals. Applied Sciences 2024, Vol. 14, Page 3237 14, 3237 (2024).

38. Kuber, P. M., Godbole, H. & Rashedi, E. Detecting Fatigue during Exoskeleton-Assisted Trunk Flexion Tasks: A Machine Learning Approach. Applied Sciences 2024, Vol. 14, Page 3563 14, 3563 (2024).

39. Hussain, I. & Jany, R. Interpreting Stroke-Impaired Electromyography Patterns through Explainable Artificial Intelligence. Sensors 24, 1392 (2024).

40. Fraser, G. D., Chan, A. D. C., Green, J. R. & Macisaac, D. T. Automated biosignal quality analysis for electromyography using a one-class support vector machine. IEEE Trans Instrum Meas 63, 2919–2930 (2014).

41. Ma, G., Zhang, J., Liu, J., Wang, L. & Yu, Y. A Multi-Parameter Fusion Method for Cuffless Continuous Blood Pressure Estimation Based on Electrocardiogram and Photoplethysmogram. Micromachines (Basel) 14, (2023).

42. Papafragkakis, A. Z., Kouroriorgas, C. I. & Panagopoulos, A. D. Performance of Micro-Scale Transmission & Reception Diversity Schemes in High Throughput Satellite Communication Networks. Electronics 2021, Vol. 10, Page 2073 10, 2073 (2021).

43. Bokal, Z. Advanced Copula-based Methods for Nonparametric Detection and Characterization of Wideband Radar Signals. Electronics and Control Systems 3, 59–66 (2024).

44. Ahmed, *, Al, M.-B., Das, S. & Khosravi, H. Binary Gaussian Copula Synthesis: A Novel Data Augmentation Technique to Advance ML-based Clinical Decision Support Systems for Early Prediction of Dialysis Among CKD Patients.

45. Examples of Electromyograms v1.0.0. Preprint at https://physionet.org/content/emgdb/1.0.0/.

46. Tao, S. et al. Deep-Learning-Based Amplitude Variation with Angle Inversion with Multi-Input Neural Networks. Processes 2024, Vol. 12, Page 2259 12, 2259 (2024).

47. Boro, N. J., Shankar, K. & Hazarika, J. A comparative analysis of EMG signals of the Healthy, Myopathy, and Low Back Pain Patients. 2022 2nd International Conference on Emerging Frontiers in Electrical and Electronic Technologies, ICEFEET 2022 (2022) doi:10.1109/ICEFEET51821.2022.9847832.

48. Elouaham, S. et al. Combination time-frequency and empirical wavelet transform methods for removal of composite noise in EMG signals. TELKOMNIKA (Telecommunication Computing Electronics and Control) 21, 1373–1381 (2023).

49. Varshney, Y. V., Chandel, G., Upadhyaya, P., Farooq, O. & Khan, Y. U. Early onset/offset detection of epileptic seizure using M-band wavelet decomposition. Int J Biomed Eng Technol 40, 205–223 (2022).

50. Farid, N. Machine Learning in Neuromuscular Disease Classification. Handbook of Metrology and Applications 1–26 (2022) doi:10.1007/978-981-19-1550-5_56-1.

51. Yan, Y. et al. Enhancing Basin-scale Hydrological Time Series Processing and Modeling with Masked Pre-Trained Encoder. Preprint at https://doi.org/10.22541/au.172417537.74282767/v1 (2024).

52. Liengaard, B. D. et al. Dealing with regression models' endogeneity by means of an adjusted estimator for the Gaussian copula approach. J Acad Mark Sci (2024) doi:10.1007/s11747-024-01055-4.

53. Ahmed, *, Al, M.-B., Das, S. & Khosravi, H. Binary Gaussian Copula Synthesis: A Novel Data Augmentation Technique to Advance ML-Based Clinical Decision Support Systems for Early Prediction of Dialysis Among CKD Patients.

54. Tao, S. et al. Deep-Learning-Based Amplitude Variation with Angle Inversion with Multi-Input Neural Networks. Processes 2024, Vol. 12, Page 2259 12, 2259 (2024).

55. Du, H.-P., Lu, Y.-X., Ai, Y. & Ling, Z.-H. BiVocoder: A Bidirectional Neural Vocoder Integrating Feature Extraction and Waveform Generation. (2024).

56. Kulkarni, P. & Madathil, D. Fully automatic segmentation of LV from echocardiography images and calculation of ejection fraction using deep learning. Int J Biomed Eng Technol 40, 241–261 (2022).

Received: October 28, 2024 / Accepted: November 20, 2024 / Published: December 15, 2024

Citation: Cepeda E, Sánchez-Pozo N, Chamorro-Hernández L. Enhanced Predictive Modeling for Neuromuscular Disease Classification: A Comparative Assessment Using Gaussian Copula Denoising on Electromyographic Data. Bionatura journal. 2024;1(2):22. doi: 10.70099/BJ/2024.01.02.22

Additional information Correspondence should be addressed to educepedam@gmail.com

Peer review information. Bionatura thanks anonymous reviewer(s) for their contribution to the peer review of this work using https://reviewerlocator.webofscience.com/

ISSN.3020-7886

All articles published by Bionatura Journal are made freely and permanently accessible online immediately upon publication, without subscription charges or registration barriers.

Publisher's Note: Bionatura Journal stays neutral concerning jurisdictional claims in published maps and institutional affiliations.

Copyright: © 2024 by the authors. They were submitted for possible open-access publication under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).